伸展树学习笔记

Posted by Songtoy on 2018-04-17
#Splay #Data Structure

伸展树($Splay$) ，一个很玄学的数据结构，据说拉伸拉着拉着就平衡了，均摊复杂度为$O(log_2n)$ ，关键在于重构、自调节。注意到关键在于$Splay()$ 部分，包含了$Rotate()$ ，剩下的部分由题目而定.

Splay

对于三种情况，

  • $u$ 的父亲为根节点，这样进行一遍单旋即可，即把$u$转上去，$Rotate(u)$

  • $u$ 的父亲不是根节点，$u$ 、父亲和祖父三点共线，此时需要先把父亲转上去，再把 $u$ 转上去.

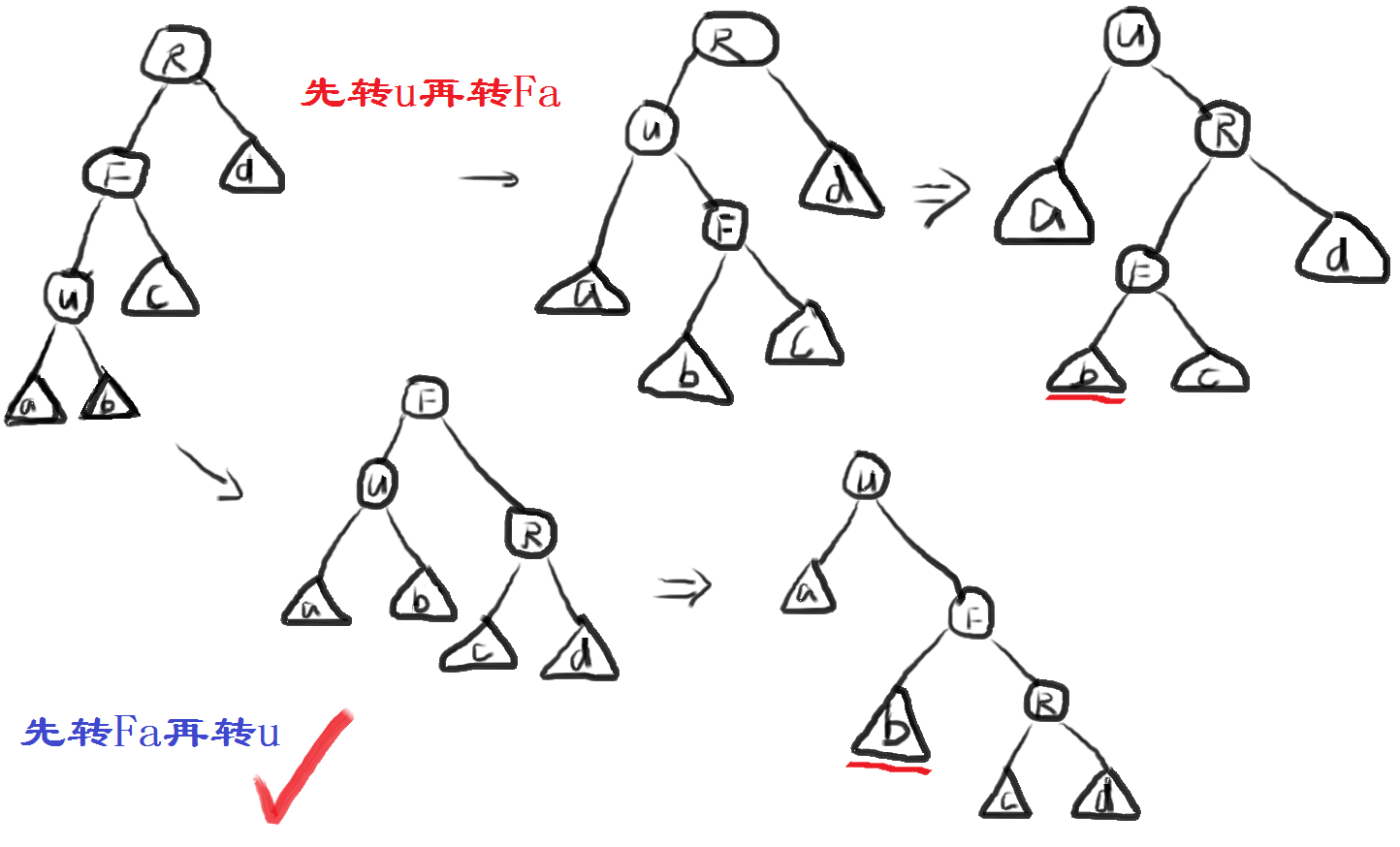    Graph(1)我们考虑$F$ 为$u$的父节点，$R$为$F$的父节点，$a、b、c、d$ 代表各个子树。两种不同的旋转过后，对于节点$u,F,R$ 对总深度的影响并不大，关键在于子树$a、b、c、d$。

    $a$ 在两种旋转后相同，$c$ 深度相同，$d$ 在第一种转法里面深度+1，在第二种转法里面深度+2，$b$ 在第一种转法里面深度不变，在第二种转法里深度-1，相比较下来第二种转法更好，更利于打散树，否则第一种转法可能会退化成一条链

  • $u$ 的父亲不是根节点，$u$ 、父亲、祖父三点不共线，此时只需要$u$ 向上转两次就好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void Splay(int p,int goal){
    top=0;
    while(p!=goal)stk[++top]=p,p=fa[p];
    while(top)Down(stk[top--]);
    p=stk[1];
    while(fa[p]!=goal){
        int F=fa[p];
        if(fa[F]!=goal){
            if(son[F][1]==p^son[fa[F]][1]==F)Rotate(p);
            else Rotate(F);
        }
        Rotate(p);
    }//代码固定
    Up(p);//Rotate时有更新各个father,这里容易忘
    if(!goal)rt=p;
}

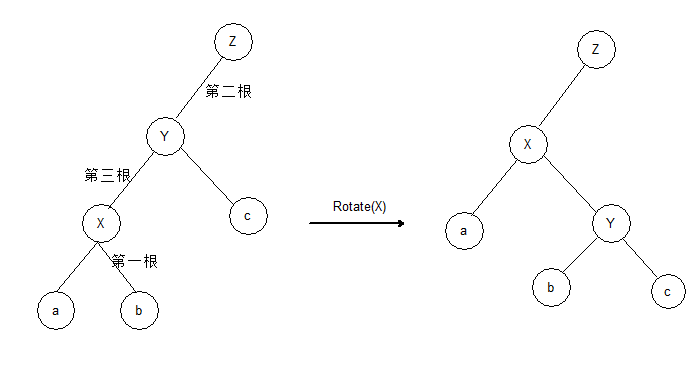
Rotate

关键在于明确左儿子还是右儿子的问题，可以借助图来推导.

Graph-rotate

1
2
3
4
5
6
7
8
9
10
11
12
void Rotate(int p){
    int F=fa[p];
    int d=son[F][1]==p;
    son[F][d]=son[p][!d];
    if(son[p][!d])fa[son[p][!d]]=F;
    fa[p]=fa[F];
    son[fa[p]][son[fa[p]][1]==F]=p;
    son[p][!d]=F;
    fa[F]=p;
    //上面代码固定
    Up(F);//这里容易忘
}

Del

先把节点$u$转到根上来，然后删除$u$之后只需要合并两子树即可，考虑$u$的儿子个数，没儿子直接删(更新$root$)，有一个儿子的话把儿子当做根，如果有两个儿子，在左子树里找到最大的数(<=val[u])，然后把这个节点转到左子树的根上，作为总根，再把$u$的右儿子接到总根上即可.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void del(int p){
    splay(p,0);
    if(son[p][0]&&son[p][1]){
        rt=son[p][0];
        fa[rt]=0;
        splay(Pre(son[p][0],val[p]),0);
        fa[son[p][1]]=rt;
        son[rt][1]=son[p][1];
    }else if(son[p][0]){
        rt=son[p][0];
    }else if(son[p][1]){
        rt=son[p][1];
    }else rt=0;
    fa[rt]=0;
    son[0][1]=rt;
    //
    fa[p]=son[p][0]=son[p][1]=0;
    --sz;
    if(!sz)rt=0;
}

还有一些必要的函数:

  • $Newnode()$

    1
    2
    3
    4
    5
    6
    7
    void Newnode(int &u,int f,ll x){
        u=++tot;
        fa[u]=f;
        mi[u]=sum[u]=val[u]=x;
        son[u][0]=son[u][1]=0;
        sz[u]=1;
    }

    ​

  • $Insert()$

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    bool Insert(int x){
        int p=rt;
        for(;;p=son[p][x>val[p]]){
            if(x==val[p]){
                splay(p);//Question Why?
                return false;
            }
            if(!son[p][x>val[p]])break;
        }
        Newnode(p,x);
        splay(tot);
        return true;
    }

    ​

  • $Pre()$

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    int Pre(int p,int x){//<=x
        int ans=-1;
        while(1){
          	Down(p);
            if(val[p]<=x){
                if(ans==-1||val[ans]<val[p])ans=p;
                if(son[p][1])p=son[p][1];
                else break;
            }else{
                if(son[p][0])p=son[p][0];
                else break;
            }
        }
        return ans;
    }

    ​

  • $Next()​$

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    int Suf(int p,int x){
        int ans=-1;
        while(1){
          	Down(p);
            if(val[p]>=x){
                if(ans==-1||val[ans]>val[p])ans=p;
                if(son[p][0])p=son[p][0];
                else break;
            }else{
                if(son[p][1])p=son[p][1];
                else break;
            }
        }
        return ans;
    }

  • $RotateTo()$

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    void RotateTo(int k,int goal){//K小的节点拉到goal下面
      /*
      由于各种可能的情况(如初始节点0，n+1、或区间翻转等)无法直接用下标访问节点，换句话说，节点的内存块发生变动，这时唯一能做的事情就是sz，对其二分即可找到第K大的节点.
      */
        int p=rt;Down(p);
        while(sz[son[p][0]]!=k){
            if(sz[son[p][0]]>k)p=son[p][0];
            else{
                k-=sz[son[p][0]]+1;
                p=son[p][1];
            }
            Down(p);
        }
        Splay(p,goal);
    }

    ​

附：基本原理

摘自Dong的博客

伸展树的出发点是这样的：考虑到局部性原理（刚被访问的内容下次可能仍会被访问，查找次数多的内容可能下一次会被访问），为了使整个查找时间更小，被查频率高的那些节点应当经常处于靠近树根的位置。这样，很容易得想到以下这个方案：每次查找节点之后对树进行重构，把被查找的节点搬移到树根，这种自调整形式的二叉查找树就是伸展树。每次对伸展树进行操作后，它均会通过旋转的方法把被访问节点旋转到树根的位置。

用Splay解决问题的时候一定要注意删除节点时对sz的影响

Splay处理问题时注意用的是权值平衡树还是下标平衡树，若是权值注意是否可能为负数

有一些题目如poj3648，维护序列,可能会访问到0，n+1，这时我们可以在开始的时候就见两个节点进去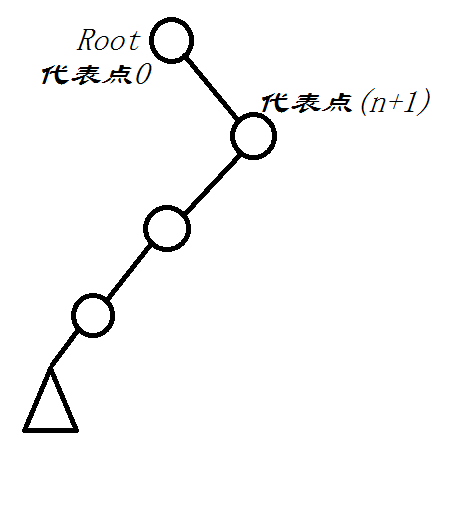splay3

例如这样，根据大小关系，我们可以确保初始的两个点分别表示0，n+1，同时利于我们对其利用sz二分查找到点(RotateTo)

模板很重要，一定要照着模板，有些地方如$Rotate()和Splay()$最后的Up部分

在把p $Splay$ 到根时注意p本身也要先down一遍,一旦有操作涉及到p的儿子(e.g.Rotate()),一定要先Down()一遍

$By SongToy$