割点，桥(割边)

割点：存在原本连通的无向图中，删去后会导致该无向图不连通的点。

割边：同上的边。

纠正：

​ 割点：去掉后使图的连通分支数增加的点.(注意是去掉整个点，而不是点周围的边)

​ 割边：图G的边e是割边当且仅当e不在任何一个圈上

$Tarjan$算法，$dfs$原图，生成搜索树，原图可表示为搜索树和一些边集，我们需要知道当前点通过非搜索树边能到达的$id$最小的点$low(u)$，此时需要维护 $u$ 掌管的子树能到达的最先遍历到的点.

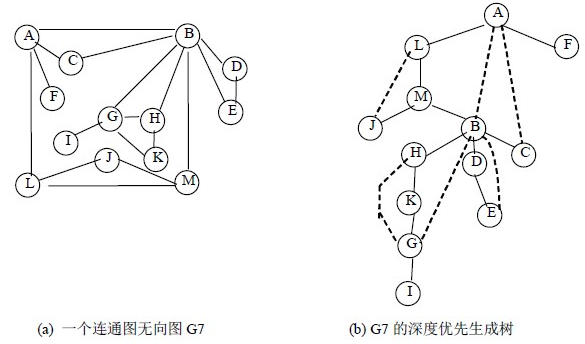
考虑两种情况：

• 1）u为根节点，则此时u为割点当且仅当u有两棵及以上搜索子树
• 2）u不是根节点，则此时一旦u存在任何一个儿子v使得$low(v)>=id[u]$，则u为割点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

void dfs(int u,int fa,int &Ind){
    int Son=0;
    low[u]=id[u]=++Ind;
    vis[u]=true;
    for(int i=head[u];~i;i=nxt[i]){
        if(to[i]==fa)continue;
        if(vis[to[i]]){
            low[u]=min(low[u],id[to[i]]);
        }else{
            dfs(to[i],u,Ind);
            if(low[to[i]]>=id[u])mark[u]=true;//该点为割点
            if(low[to[i]]>id[u])ans[i]=true;//该边为割边
            low[u]=min(low[u],low[to[i]]);
            ++Son;
        }
    }
    if(id[u]==1&&Son<=1)mark[u]=false;//如果是根节点的话考虑有多少个儿子
}

强连通

强连通分量：在有向图中一个子图，其内部任意两点均可相互到达，并使该子图最大

(这里撇去以前的$kosaraju$写法)

$Tarjan$ ：按照 $dfs$ 搜索树，如果当前节点的子树中没有任何边指向子树外的内容，则我们能确保当前的子树内的强连通情况与子树外完全没有关系，(根本不能相互到达)，那么我们还剩余在栈中的所有元素就是u所在的强连通分量的所有元素。换句话说，当前栈里剩余的元素的$low(v)$一定在$v$的前面，我们只需要递归回到那个节点的时候把所有的元素收集起来就好. $O(n+m)$

注意点:

由于是有向图，因此当前搜索到的子图有可能有边指向以前的已经搜过的点，例如下图中我们在红色点考虑蓝色点，蓝色点的$dfn$ 必然会导致红色点的$low$比右边任何点的$dfn$都小，这将导致右边的强连通分量无法被求出来.

因此，要确保当前的搜索过程一定在还未确定强连通分量的子图中进行，需要区分已经处理的点和还未处理的点，我们只需要考虑栈中的元素即可，(因为假如有别的子图还未被遍历过，这里的点一定不可能在当前的子图的强连通分量中，不需要考虑)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

void dfs(int u,int &Ind,int &k){
    vis[u]=true;//in stack
    low[u]=dfn[u]=++Ind;
    stk[++top]=u;
    for(int i=0;i<G[u].size();i++){
        if(vis[G[u][i]]&&dfn[G[u][i]]){//
        	low[u]=min(low[u],dfn[G[u][i]]);
        }
        else if(!dfn[G[u][i]]){
            dfs(G[u][i],ind,k);
            low[u]=min(low[u],low[G[u][i]]);
        }
    }
    if(low[u]==dfn[u]){
    	++k;//scc_id_top
    	while(top){
    		int v=stk[top--];
    		sccid[v]=k;
    		vis[v]=false;
            if(Mi[k]==-1||Mi[k]>val[v])Mi[k]=val[v];
            Mx[k]=max(Mx[k],val[v]);
            if(v==u)break;
        }
        dp[k]=Mx[k]-Mi[k];
    }
}

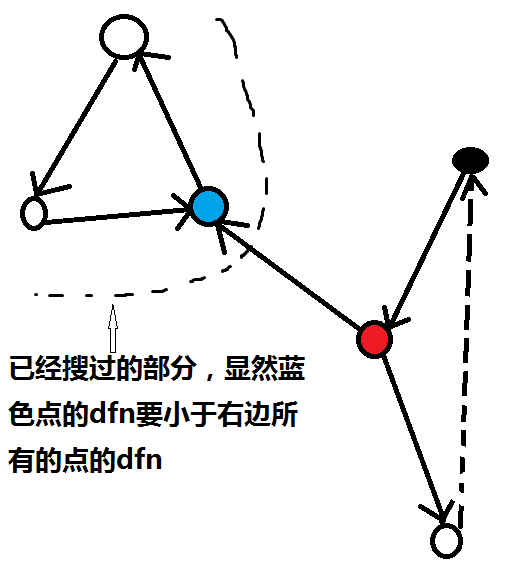
Ps : Lowest Common Ancester

运用RMQ求解的Lca,注意：预处理复杂度$O(nlogn)$,求解复杂度$O(1)$

引入:欧拉序列

与$dfs$序不同的是，$dfs$序表示的是每个点被加入栈的顺序)，但是欧拉序列表示的是栈顶中的元素的序列，$dfs$序中一个$[st[u],ed[u]]$只能表示其子树内的元素并且长度恰等于子树内的元素的个数，然而欧拉序列中$[st[u],ed[u]]$不仅仅是表示子树内的元素，即，($st[u]$表示$u$初次出现的位置，$ed[u]$表示$u$最后一次出现的位置)，我们能确保$[st[u],ed[u]]$中的元素只可能是$u$的子孙和$u$本身，但是同时还有一个$dfs$遍历的顺序.

$Function\;Dfs(u,\&tot)\{$

​ $euler.add(u)$

​ $st[u]=++tot$

​ $for\;v\;in\;\{son[u]\}\;do$

​ $Dfs(v,tot)$

​ $euler.add(u)$

​ $done$

$\}$

通过这段伪代码可以知道，欧拉序列实际上就是每条边遍历的顺序及方向，(任意相邻位置上的两点均为某边的两端).

这样一来，$lca(u,v)$就是在$[ed[u],st[v]]$中$dep$值最小的点，那么我们只需要维护一个区间最小值即可，可以用$ST$表解决，然后查询的时候，非常漂亮的一步就是我们不再使用倍增的写法$O(logn)$，直接$O(1)$判断，由于是区间最小值，对于区间$[L,R]$，只需要求出$[L,x]$和$[y,R]$$(x>=y)$的最小值即可，那么我们只需要求出最小的长度使得其两倍能覆盖$[L,R]$即可，i.e:$2^{len}*2>=R-L+1$，这里的$len$可以预处理出来:

1
2
3
4

for(int i=2;i<=tot;++i){//Log[1]=0
  	Log[i]=Log[i-1];
 	if(i==(i&-i))++Log[i];
}

$ST$表的预处理部分：

1
2
3
4
5
6
7
8
9

for(int i=1;i<=tot;++i)mi[0][i]=eu[i];
for(int j=1;j<S;++j){
    for(int i=1;i<=tot;++i){
        mi[j][i]=mi[j-1][i];
        if(i+(1<<(j-1))<=tot&&dep[mi[j][i]]>dep[mi[j-1][i+(1<<(j-1))]]){
            mi[j][i]=mi[j-1][i+(1<<(j-1))];
        }
    }
}

查询的时候还有一个小技巧,由于$[st[u],ed[u]]$中只有$u$的子树和$u$本身，那么其中$dep$最小的一定是$u$，那么其实只要查询$[st[u],st[v]]$中的最小深度元素，对答案不构成影响。

虚树

在处理一些问题的时候，有时候往往要将一部分满足条件的点提出来单独处理，但是这个时候如果仍旧$O(n)$扫描是不明智的，考虑能否造出一颗虚树

主要解决树上每次询问k个关键点，满足∑k是线性的问题

Defination

所谓虚树，即将所需的点都提取出来，并用”虚边”将其连接起来，同时保留了所有点的相对位置(如LCA，虚边的长度)，即其中对答案有影响的信息.

Construction

将所有的点按照$Dfs$序排序，然后将任意相邻两点的$Lca$加到集合中，整合一下即可得到一颗虚树所需的点集.

• i.e：将所有点按照$dfn$排序后，{相邻两点Lca}={任意两点Lca}
• Proof: