旅行

Posted by Songtoy on 2017-09-04
#Graph Theory #Two pointers #Binary

Solution

令 $dis[u]$ 表示u到根节点的路径的”长度”并且满足 $dis[u]=edge(u,fa)-dis[fa]$ .

考虑可行路径u,v，他们的 $LCA$ 为 $lca$ ，则

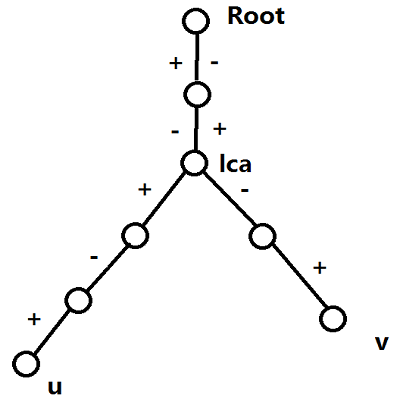
Graph

如图，路径左侧表示的是$u$到$Root$路径上每一条边的长度的加减情况，可以得到，由于$(dep[u]-dep[v])\%2==0$ ，$Length(u,v) = dis[u]+dis[v]$ ，因此，我们只需要把所有的点按 $dep[]$ 的奇偶性分成两类，得到两个$dis$的数组，由于要求的是第$K$小的路径，我们二分答案的路径长度，然后求出有多少条路径”长度”小于等于 $limit$ (即 $mid$ )$ ，这一步可以用归并两个有序数组解决。

对奇数一组每个i，我们每次维护最后一个满足 $dis[i]+dis[j]<=lmt$ 的 $j$ ，由于两个数组均为有序，$i$ 向右推进的过程中，$j$ 一定会逐渐变小，因此问题即可解决。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
static const int M = 100005;
ll dis[M];
ll Div[2][M];
int dep[M],st[M],ed[M],obj[M];
ll len[M*10];
struct node{
    int to,cost;
    node *nxt;
    void push_back(int v,int c){
        node *p=new node;
        p->to=v;
        p->cost=c;
        p->nxt=nxt;
        nxt=p;
    }
}es[M];
struct Big{
    int cnt[2];
    Big(){
        memset(cnt,0,sizeof(cnt));
    }
    void dfs(int u,int fa){
        for(node *i=es[u].nxt;i;i=i->nxt){
            int v=i->to;
            if(v==fa)continue;
            dep[v]=(dep[u]+1)&1;
            dis[v]=(ll)(i->cost)-dis[u];
            dfs(v,u);
        }
    }
    bool check(ll lmt,int K){//cnt(<=lmt) >=K)
        ll ans=0;
        int j=cnt[0];
        for(int i=1;i<=cnt[1];++i){//dis[x]+dis[y]<=lmt
            while(j>=1&&Div[0][j]+Div[1][i]>lmt)--j;//last element j which satisfies Div[0][j]+Div[1][i]<=lmt
            ans+=j;
        }
        return ans>=K;
    }
    
    void solve(int n,int K){
        dfs(1,1);
        for(int i=1;i<=n;++i){
            Div[dep[i]][++cnt[dep[i]]]=dis[i];
        }
        sort(Div[0]+1,Div[0]+cnt[0]+1);
        sort(Div[1]+1,Div[1]+cnt[1]+1);
        ll L=-1ll<<50,R=1ll<<50,ans=1ll<<50;
        while(L<=R){
            ll mid=L+R>>1;
            if(check(mid,K))ans=mid,R=mid-1;
            else L=mid+1;
        }
        if(ans>=1ll<<50)puts("Stupid Mike");
        else cout<<ans<<endl;
    }
}Grand;
int main(){
    int n,K;
    rd(n),rd(K);
    for(int i=1,u,v,c;i<n;++i){
        rd(u),rd(v),rd(c);
        es[u].push_back(v,c);
        es[v].push_back(u,c);
    }
    Grand.solve(n,K);
    return 0;
}

个人总结

处理这一题的时候看到小数据为1000，直接暴力枚举可以达到$O(n^2)$，用dfs序即可，每次枚举节点$u$一个儿子的子树内的点与u子树中除该儿子外的子孙节点，表面上是$O(n^3)$ ，但是实际上是枚举点对，只有$O(n^2)$ 。

同时发现路径$(u,v)$的$Length$其实就等于$dis[u]+dis[v]$ ，那么我们就不需要枚举子树了，只需要求出所有点的$dis$ ，根据奇偶性放到两个数组里，枚举任意点对即可。

由于最后要求的是第$K$短的路径，一个比较可行的想法是二分，在边界上处理完了之后卡在了$check()$上，并没有想到可以归并求解，当时的目的是找到所有$dis[i]+dis[j]>=lmt$的点对$(i,j)$ 个数ans，并判断$ans>=K$是否成立，觉得应该可以用map什么的解决，但是时间已经不够了，思路越加混乱。

应该注意这类问题，往往和两个元素有关，可能是相加、相乘，这个时候可以考虑一下归并，一方面可以像这样二分求解，另一方面可以借用优先队列，在$K$有限的情况下存下所有的路径，每次找到最小的元素，具体如下：

刚开始存下所有的
$$a_1+b_1, a_1+b_2, .. ,a_1+b_n$$
然后每次取出最小的元素，再放进一个元素越靠近这个元素越好，不妨为$min(a_{i+1}+b_{j} , a_i+B_{j+1})$ ，这样能确保复杂度。

$By SongToy$